Machine Learning
Understanding the Directional Derivative and the Gradient
1 Introduction Understanding how functions change in different directions is crucial in many fields. For example in the context of neural networks where gradients are used to update weights during
Machine Learning, Math
Mastering the Softmax Function: Understanding its Derivative with a Step-by-Step Example
\title{Mastering the Softmax Function: Understanding its Derivative with a Step-by-Step Example} \maketitle This article focuses on obtaining the derivative of the softmax function by means of a simple example. It
Machine Learning
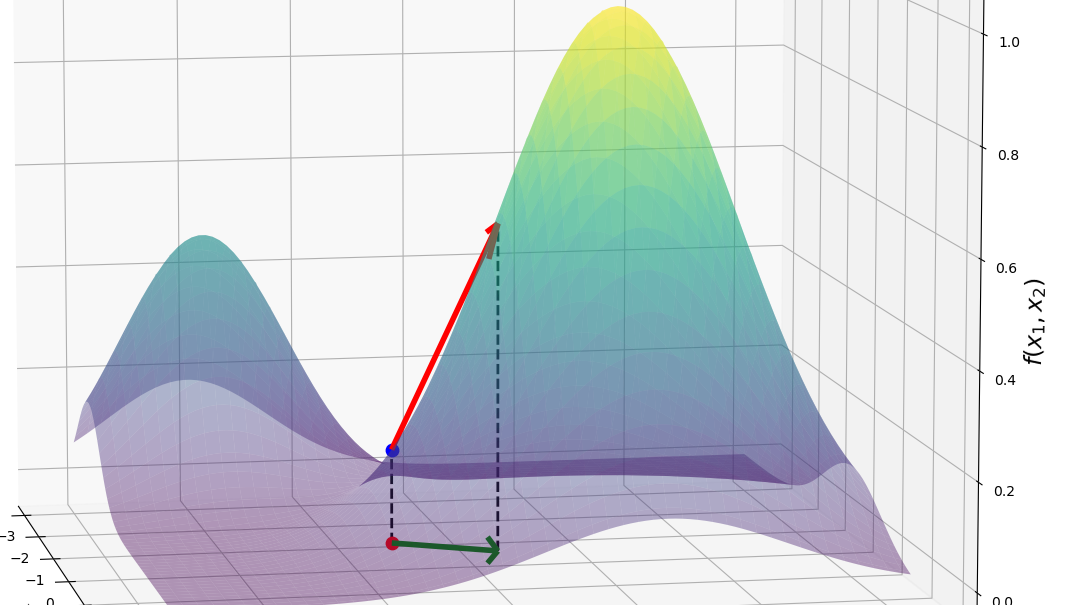
The Sigmoid and its Derivative
The simoid function, $\sigma(x)$, is also called the logistic function, or expit \textcite{wiki_logit}. It is the inverse of the logit function. It’s function definition is:\begin{equation}\sigma(x) = \frac{1}{(1+e^{-x})}%\tag{sigmoid function}\label{eqn:sigmoid}\end{equation} Let’s get
Machine Learning
What is a Logit?
The term logit has different meanings in math and in the TensorFlow library. In Ten-sorFlow it means “Per-label activations, typically a linear output. These activation energies are interpreted as unnormalized
Bayesian Methods
Expectation Maximization
https://stats.stackexchange.com/questions/72774/numerical-example-to-understand-expectation-maximization http://noiselab.ucsd.edu/ECE228/Murphy_Machine_Learning.pdf https://bjlkeng.github.io/posts/the-expectation-maximization-algorithm/