The Sigmoid and its Derivative

The simoid function, $\sigma(x)$, is also called the logistic function, or expit \textcite{wiki_logit}. It is the inverse of the logit function. It’s function definition is:
\begin{equation}
\sigma(x) = \frac{1}{(1+e^{-x})}
%\tag{sigmoid function}
\label{eqn:sigmoid}
\end{equation}

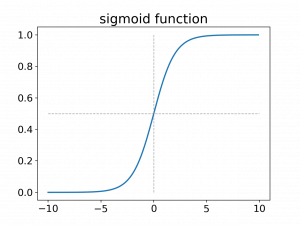
Let’s get familiar by plotting this function first:

A plot of the sigmoid function.

And just to be complete, here is the python code that produced the above plot:

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots(1,1)
x=np.arange(-10,10,0.1)
y=1/(1+np.exp(x))
ax.plot(x,y)
ax.set_title("sigmoid function", fontsize=20)
ax.tick_params(axis="x", labelsize=15)
ax.tick_params(axis="y", labelsize=15)
xs = np.linspace(1, 20, 10)
ys = np.linspace(0, 1, 1)
ax.hlines(y=0.5, xmin=-10, xmax=len(xs), colors='gray', linestyles='--', lw=1, alpha=0.7)
ax.vlines(x=0, ymin=0, ymax=len(ys), colors='gray', linestyles='--', lw=1, alpha=0.7)
plt.show()
fig.savefig("sigmoid", dpi=200, transparent=True)

We see that the sigmoid function maps from the real numbers to the $[0,1]$ interval which can be interpreted as a probability.
\begin{equation}
f(L): [-\infty, \infty ]\mapsto [0,1]
\end{equation}.

This and the fact that it is differentiable makes the sigmoid very suitable to be used with neural networks.
Our goal now is to compute the derivative and write it in terms of $\sigma(x)$ – you will see what I mean by that in a bit. So here we go. First we bring the formula into
a slightly different form which is more suitable for doing the derivative:

\begin{equation}
\begin{aligned}
\frac{1}{(1+e^{-x})} &= \frac{e^{x} }{e^{x}(1+e^{-x})} & \hspace{2cm} \text{expand the fraction by $e^x$}\\
&=\frac{e^{x}}{e^x + e^xe^{-x}} = \frac{e^{x}}{e^x+e^{0}} = \frac{e^{x}}{e^x + 1} \\
%\tag{sigmoid function}
\end{aligned}
\end{equation}

Now we do the derivative:

\begin{align}
\frac{d}{dx}\left(\frac{e^{x}}{e^x + 1}\right) &=\frac{{e^{x}}^{\prime}(e^x+1) – (e^x+1)^{\prime} e^x}{(e^x+1)^2} \tag{1}\label{eq:eq1} \\
& =\frac{e^x(e^x-1) – e^x e^x}{(e^x+1)^2} \tag{2}\label{eq:eq2} \\
& =\frac{e^x(e^x+1)}{(e^x +1)(e^x +1)} – \frac{e^x e^x}{(e^x +1)(e^x +1)} \tag{3}\label{eq:eq3} \\
& =\sigma(x) – \sigma(x)^2 = \sigma(x)(1 – \sigma(x)) \tag{4}\label{eq:eq4}
\end{align}
In line $\eqref{eq:eq1}$ we apply the chain rule. In line \eqref{eq:eq3} we substitute $\sigma(x) = \frac{e^x}{e^x+1}$ and in line \eqref{eq:eq4} we factor out $\sigma(x)$.
And this is it. This is the derivative of the sigmoid function in terms of itself, i.e. $\sigma(x)$. To finish this up, we plot its derivative in figure 2.

And this is it. This is the derivative of the sigmoid function in terms of itself, i.e. $\sigma(x)$. To finish this up, we plot its derivative.

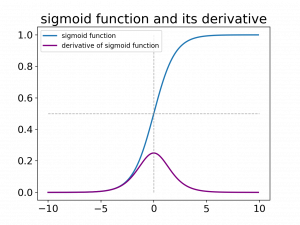References
[1] https://en.wikipedia.org/wiki/Logistic_function.

Was this helpful?

YesNo

1 / 0