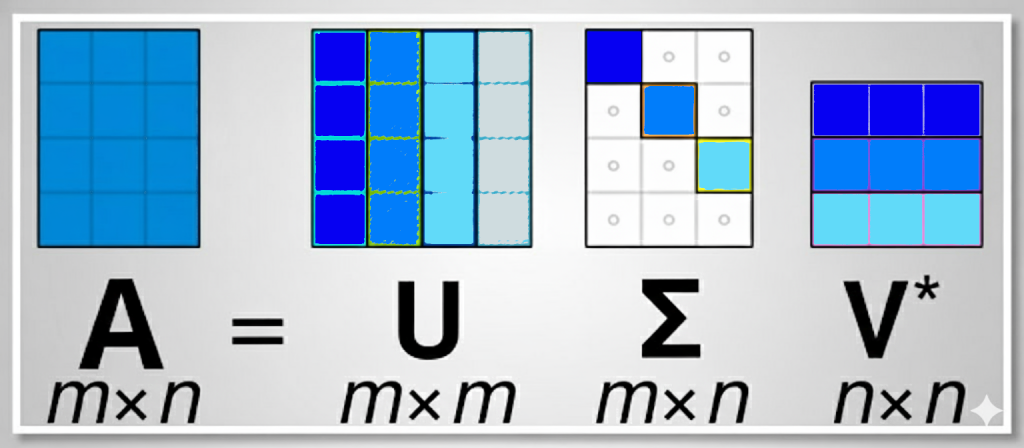
Introduction
The Singular Value Decomposition (SVD) is “a highlight of linear algebra” to quote Prof. Strang ( [1] p. 371). However, I must confess that when I studied it I had a difficult time understanding it and this was due to how it was presented. The SVD is often introduced as a given formula which is then shown to just work. But it always felt very unsatisfying to me not knowing why. So – here is the SVD explained the way I wish I had been taught, which is deriving it from first principles.
Preliminaries
It is very important to understand the concepts that the SVD builds on. Thus, here is a list of topics that you should be “good friends” with and to make it easy for you if they feel a bit rusty, I’ve linked my previous guides along with the main message you’ll need for this article. When you have a good understanding of spectral decomposition you are good to go.
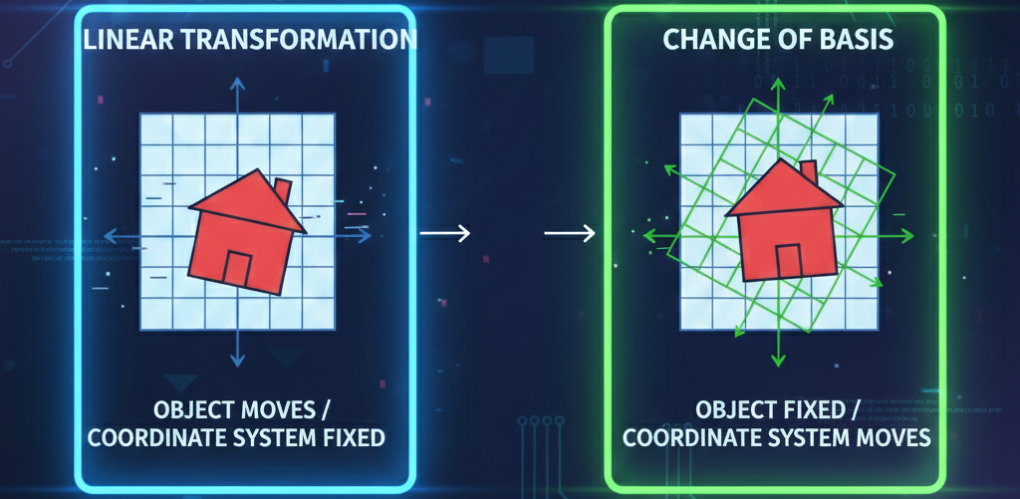
Key point: Multiplying a vector by the inverse of a basis matrix represents a change of basis. The vector itself doesn’t change, but we are now expressing it in a different coordinate system.
Key point: Eigenvectors are specific to a matrix. They are unique because they do not change their direction when transformed by that matrix; they only get scaled by the eigenvalues. If a matrix \(\mathbf{A}\) has enough linearly independent eigenvectors we can collect these in a matrix \(\mathbf{B}\) and they form a basis for the vector space that \(\mathbf{A}\) lives in. We call \(\mathbf{B}\) an eigenbasis of \(\mathbf{A}\). In some cases the eigenvectors in the eigenbasis are even orthogonal and that has some really nice properties, which we exploit when diagonalizing symmetric matrices.
Key point: If a square matrix \(\mathbf{A}\) has an eigenbasis \(\mathbf{B}\) we can simplify any transformation \(\mathbf{Ax}\) by first expressing \(\mathbf{x}\) in terms of the eigenbasis (by computing the change of basis \(\mathbf{B}^{-1}\mathbf{x}\)), scaling it by the eigenvalues, and then transforming it back to the standard basis. Not all matrices can be diagonalized this way, usually, certain conditions (like having \(n\) linearly independent eigenvectors) are required.
Why orthogonal matrices rotate and diagonal matrices stretch
Key point: This is the diagonalization of symmetric matrices. Symmetric matrices are special. They can ALWAYS be diagonalized. In addition, their eigenbasis is always orthogonal. Once normalized, this basis becomes orthonormal, which gives us the beautiful property that the inverse is simply the transpose: \(\mathbf{Q}^{-1} = \mathbf{Q}^\mathbf{T}\). Because of this, the diagonalization has a very nice geometric interpretation. The action of the matrix \(\mathbf{A}\) on a vector \(\mathbf{x}\) is decomposed into: a) the vector is expressed in the eigenbasis of the \(\mathbf{A}\) by a mere rotation, i.e. the required change of basis equals a rotation. b) Once \(\mathbf{x}\) is expressed in the coordinates of the eigenbasis, the action of \(\mathbf{A}\) reduces to a simple stretch. c) It then gets rotated back into the original vector space, i.e. the second change of basis also reduces to a rotation. It is important to note, that the change of bases operations do not alter the length of \(\mathbf{x}\). The only operation that does that is the diagonal matrix which does the stretching. Therefore we say that all the “energy” (the stretching) is contained in the diagonal matrix.
The Problem to Solve
I believe concepts are best understood if we understand what problem they were developed to solve. So what is the problem? Matrix diagonalization (factoring a matrix into the product of matrices where one is diagonal) is great for several reasons: it eases computations, it allows to understand the actions of a matrix better, and when we write the factorization as a sum of outer products, we can use it for approximation tasks (think of principal component decomposition, PCA). So we want matrix diagonalization. Sadly, only specific matrices can be diagonalized and it is not always easy to find out which ones.
However, if a matrix is symmetric then we know straight away that not only can it be diagonalized into \(\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^T\), but also that \(\mathbf{Q}\) is orthonormal which makes all the energy go into the diagonal matrix, which is a very clean decomposition. The other two matrices are square and orthonormal which means they perform rotations.
If only we could have this for any matrix, not only symmetric ones! This is the problem we want to solve and you’ve guessed it – the SVD is the solution to this problem.
The Strategy
Let’s pretend for a moment the SVD didn’t exist and we were given the task to solve this problem. Let’s think about how we could achieve this based on the information we already have: We start off with a matrix \(\mathbf{A}\in \mathbb{R}^{m \times n}\) and what we want is an expression like \[\begin{aligned} \mathbf{A} = \mathbf{B D C} \end{aligned}\] thus a diagonal matrix \(\mathbf{D}\) and two other matrices \(\mathbf{B}\), and \(\mathbf{C}\). In particular, we want \(\mathbf{B}\) and \(\mathbf{C}\) to be bases which are square and orthonormal to have a clear “separation of concerns,” just like we do when dealing with spectral decomposition. Now we have defined what we have and what we want.
Now, how to go about this? Apparently being symmetric is a superpower for a matrix. But \(\mathbf{A}\) is not symmetric. But wait – at least we can derive a symmetric matrix from it simply by multiplying \(\mathbf{A}\) with its own transpose from the left or right. So if \(\mathbf{A}\) \(\in \mathbb{R}^{m \times n}\), then \(\mathbf{AA}^T\) \(\in \mathbb{R}^{mxm}\) and \(\mathbf{A}^T\mathbf{A}\) \(\in \mathbb{R}^{nxn}\) are symmetric matrices. We know that both of \(\mathbf{AA}^T\) and \(\mathbf{A}^T\mathbf{A}\) can be diagonalized and that they each have an orthogonal basis (since they are symmetric).
Can we do something with this information? Once again, we want to express the actions that \(\mathbf{A}\) applies to a vector \(\mathbf{x}\) to be expressed as a sequence of operations: \[\begin{aligned} \mathbf{Ax} = \mathbf{B D Cx} \end{aligned}\] We have already stated that the left matrix \(\mathbf{B}\) and the right matrix \(\mathbf{C}\) should be orthogonal bases. Why not use the basis of either \(\mathbf{AA}^T\) or \(\mathbf{A}^T\mathbf{A}\). Which one could be applied to \(\mathbf{x}\)? remember that \(\mathbf{x}\) \(\in \mathbb{R}^n\)? Only the basis of \(\mathbf{A}^T\mathbf{A}\), let’s call it \(\mathbf{V}\), can multiply it because \(\mathbf{V}\) is \(\in \mathbb{R}^{nxn}\). We could apply a change of basis to \(\mathbf{x}\) to express it in the coordinates determined by \(\mathbf{V}\). To do so we must multiply \(\mathbf{x}\) by the inverse, \(\mathbf{V}^{-1}\). Since in this case the eigenbasis is orthonormal we know its inverse equals its own transpose. Convenient. But not a coincidence, we chose a symmetric matrix precisely for this reason. So we can compute \(\mathbf{V}^T \mathbf{x}\) and the result is the same \(\mathbf{x}\) expressed in a different reference system.
Recall that we want an equation that has \(\mathbf{Ax}\) on the left side. To be able to write this, we would have to undo the change of basis because \(\mathbf{A}\) expects a vector expressed in standard normal coordinates not the coordinates of some other basis. Of course, that is easy; we just undo the change of basis by multiplying by \(\mathbf{V}\), so we have \(\mathbf{V}\mathbf{V}^T \mathbf{x}\). This is a bit like expanding an expression e.g. saying \(a = a +1-1\). So this is what it looks like:
\[\begin{aligned} \mathbf{Ax} = \mathbf{AV}\mathbf{V}^T \mathbf{x} \end{aligned}\] We are making progress. What is missing? Oh – no diagonal matrix yet. Also, we need another orthonormal basis. Let’s have a closer look at \(\mathbf{AV}\).
We know that the column vectors in \(\mathbf{V}\), the \(\mathbf{v}_i\) are the eigenvectors of \(\mathbf{A}^T\)\(\mathbf{A}\) and therefore by definition \[\begin{aligned} \mathbf{A}^T\mathbf{A}\mathbf{v}_i = \lambda_i\mathbf{v}_i\end{aligned}\] where \(\lambda_i\) is the corresponding eigenvalue.
We also know that \(\mathbf{V}\) is an orthonormal basis. That means that the dot product of any two different column vectors of \(\mathbf{V}\) will be 0 and the dot product of the same column vectors equal 1.
Does this get changed when multiplying it by \(\mathbf{A}\)?
We need to check if \((\mathbf{Av}_i)^\mathbf{T}\mathbf{Av}_j=0\) for \(i\neq j\): \[\begin{aligned} (\mathbf{Av}_i)^\mathbf{T} \mathbf{Av}_j &= \mathbf{v}_i^\mathbf{T} \mathbf{A}^\mathbf{T} \mathbf{Av}_j \ &= \mathbf{v}_i^\mathbf{T}(\mathbf{A}^\mathbf{T} \mathbf{A})\mathbf{v}_j \ &= \mathbf{v}_i^\mathbf{T} \lambda_j\mathbf{v}_j \ &= \lambda_j\mathbf{v}_i^\mathbf{T}\mathbf{v}_j = 0\end{aligned}\]
If \(i=j\) we would have \(\lambda_i\mathbf{v}_i^T\mathbf{v}_i =\lambda_i\) Wow! So \(\mathbf{AV}\) IS still an orthogonal eigenbasis. Only – it is not orthonormal, we have just shown that the lengths of the vectors are \(\sqrt{\lambda_i}\) and not 1. (Why is the length \(\sqrt{\lambda_i}\)? Because the dot product of a column vector \(v_i\) of \(\mathbf{AV}\) with itself was shown to be \(\lambda_i\) and the length of a vector is defined to be the square root of its dot product.) That is easy to fix, we just divide each column vector by its corresponding length, i.e. the square root of the eigenvalue, \(\sqrt{\lambda_i}\). Actually – it is tedious to always say “the square root of the eigenvalues of \(\mathbf{A}^T\mathbf{A}\), from now on I’ll refer to these as singular values and denote them as \(\sigma_i\). But back to the normalization. We can write this elegantly in matrix notation; we can construct a new matrix, \(\mathbf{\Sigma}^{+}\) of the same shape as \((\mathbf{A}\mathbf{V})^T\) and we place the reciprocal of the singular values on its diagonal. For example, if \(\mathbf{A}\mathbf{V}\in\mathbb{R}^{3,2}\), then \(\mathbf{\Sigma}^{+}\) will have the same shape and the last row will be zeros, see below:
\[\begin{aligned} \begin{pmatrix} \frac{1}{\sqrt{\lambda_1}} & 0 \\ 0 & \frac{1}{\sqrt{\lambda_2}}\\ 0 & 0 \\ \end{pmatrix} \label{eq:sig}\end{aligned}\] (Note, the above matrix fullfills the concept of an inverse, but since \(\mathbf{\Sigma}\) is not square it doesn’t have a real inverse. What we constructed above is called the Moore-Penrose pseudo-inverse) Only now the equality in our equation \(\mathbf{A}\mathbf{x}= \dots\) doesn’t hold anymore, because we divided the right side by \(\mathbf{\Sigma}\), thus we need to undo this again, just like before when we undid the change of basis operation. To undo this, we simply multiply by \(\mathbf{\Sigma}\). With this we get: \[\begin{aligned} \mathbf{Ax} = \mathbf{AV\Sigma}^{+}\mathbf{\Sigma}\mathbf{V}^T\mathbf{x} \end{aligned}\] This is really exciting, because now we have all the pieces we wanted! We just rearrange this term a bit by naming \(\mathbf{\hat{U}}=\mathbf{AV\Sigma}^{+}\). Now we have \[\begin{aligned} \mathbf{Ax} = \mathbf{\hat{U}}\Sigma\mathbf{V}^T\mathbf{x} \end{aligned}\] Et voilà! This is the formula for the SVD – well, almost! It is what you get when you make the following call in Python:
# Thin SVD (returns U as m x n)
U, S, Vh = np.linalg.svd(A, full_matrices=False)Note, that the matrix \(\mathbf{\hat{U}}\) is not necessarily a square matrix. But we need a square matrix, or rather – we want a square matrix, because we wanted a clear “separation of concerns”. We wanted a rotation a stretch and another rotation. A rotation matrix must be square, because it must have an inverse. If we rotate in one direction, we will need to be able to rotate back. If we tried to do this with a let’s say \(2 \times 4\) matrix, we would map from 4-d to 2-d. We would loose information, we could never go back to the original.
There are methods to complete an orthonormal basis, e.g. using the Gram-Schmidt process if \(\mathbf{A}\) is tall and thin. However, I won’t go into details here, because the important thing in my opinion is that we can start with \(\mathbf{A}^T\mathbf{A}\) and all the rest follows from this. Note that the additional columns we use to complete \(\mathbf{U}\) into a square matrix must be orthogonal to the already-computed columns of \(\hat{\mathbf{U}}\). One natural choice is to take them from the null space of \(\mathbf{A}^T\), since any vector in the null space of \(\mathbf{A}^T\) is orthogonal to the column space of \(\mathbf{A}\), which is exactly where the columns of \(\hat{\mathbf{U}}\) live.
In Python we compute the full (square \(\mathbf{U}\)) SVD like this:
# Full SVD (returns U as m x n)
U, S, Vh = np.linalg.svd(A, full_matrices=True)Now, we have finally reached our goal, we arrived at the decomposition with two orthonormal basis matrices \(\mathbf{U}\) and \(\mathbf{V}^T\). Remember that we call the entries in \(\mathbf{\Sigma}\) singular values. Accordingly we call the vectors in \(\mathbf{U}\) the left singular vectors of \(\mathbf{A}\) and the vectors in \(\mathbf{V}\) the right singular vectors. They form a triplet as we will see in the following paragraph.
Order Matters
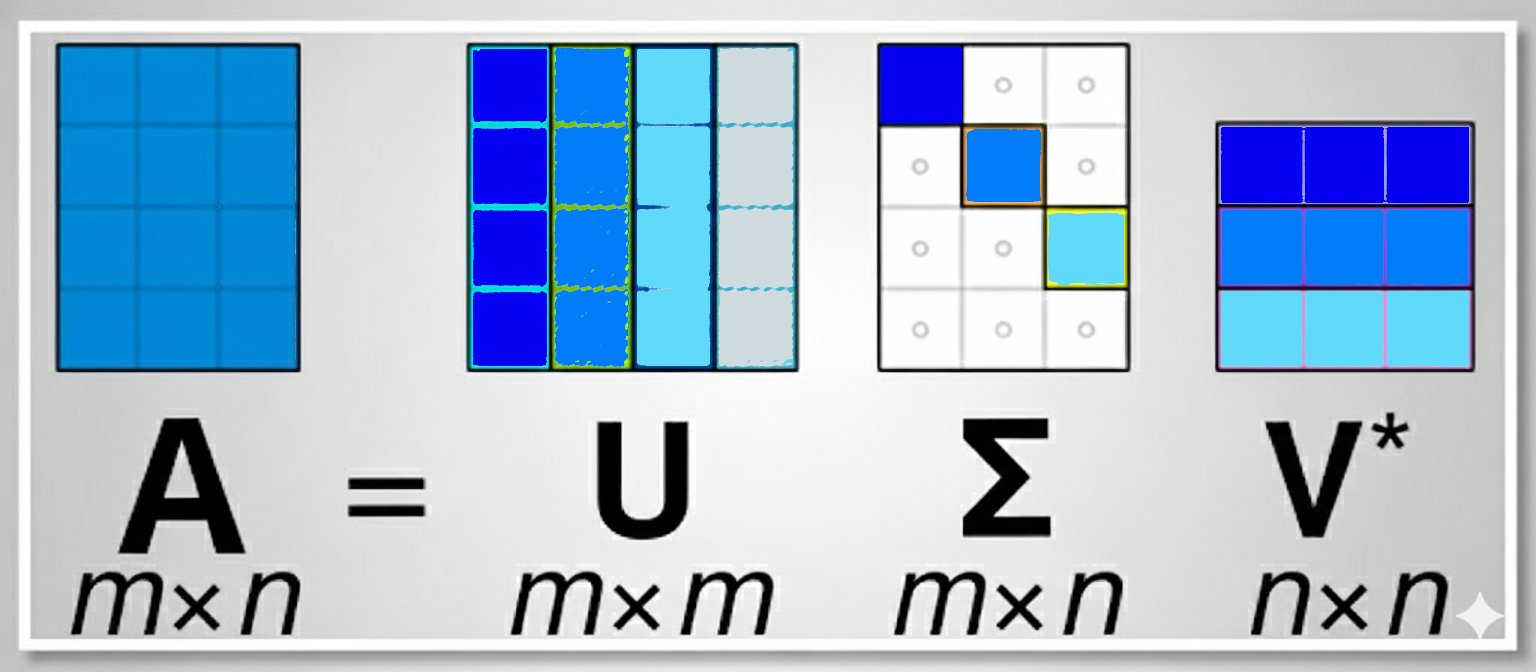
Recall that \(\mathbf{V}\) constitutes the eigenbasis for \(\mathbf{A}^T\mathbf{A}\). It’s crucial to understand that they are paired with their corresponding eigenvalue and thus the derived singular value in \(\mathbf{\Sigma}\) and therefore also with the corresponding left singular vector which is derived from this. To illustrate this, I’ve color-coded these relationships in Figure 1. For instance, \(\mathbf{u}_1\), \(\sigma_1\), and \(\mathbf{v}^T_1\) form a single set, where the lower case letters \(\mathbf{u}\), and \(\mathbf{v}\) indicate a column of \(\mathbf{U}\) and \(\mathbf{V}\), respectively. And similiary \(\mathbf{u}_2\), \(\sigma_2\), and \(\mathbf{v}^T_2\) form a set, and so on.
We can reorder these components as long as we don’t break the triplets, for example, we could swap the third column of \(\mathbf{U}\) with the first column of that matrix, but then we would also need to swap \(\sigma_3\) with \(\sigma_1\), as well as \(\mathbf{v}^T_3\) with \(\mathbf{v}^T_1\). By convention, when computing the SVD, the singular values are arranged in descending order (\(\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_n\)), which consequently dictates the ordering of the singular vectors in \(\mathbf{U}\) and \(\mathbf{V}\). This organization is crucial for approximation tasks.
We have just stated that by convention the ordering of the singular values is in descending order. Now we will see why this is important. Recall that matrix multiplication can be seen as a sum of the outer products (see herefor a reminder). Thus we can write: \[\mathbf{A} = \mathbf{U}\mathbf{\Sigma} \mathbf{V^T} = \mathbf{u}_1\mathbf{\sigma}_1\mathbf{v}_1^T + \mathbf{u}_2\mathbf{\sigma}_2\mathbf{v}_2^T \dots \mathbf{u}_r\mathbf{\sigma}_r\mathbf{v}_r^T\] (The number \(r\) is the number of singular values- it equals the rank of \(\mathbf{A}\).) The term, \(\mathbf{u}_1\mathbf{\sigma}_1\mathbf{v}_1^T\) represents the matrix \(\mathbf{u}_1\mathbf{v}_1^T\) weighted by \(\sigma_1\). And this is really significant! It tells us that we can rewrite the matrix \(\mathbf{A}\) as a sum of rank 1 matrices. A rank one matrix is one where all columns are multiples of a single column, or all rows are multiples of a single row. All matrices resulting from an outer product (column vector times row vector) have a rank of 1.
Since \(\mathbf{u}_i\) and \(\mathbf{v}_i\) (for \(i=1\) to \(r\)) are of unit length, due to their orthonormality, the singular values act as weights. The larger the corresponding singular value, the This is where the ordering creates the (mathe)magic: If we sum only the first few rank 1 matrices with the largest singular values these will be most important for reconstructing \(\mathbf{A}\). We can drop all the remaining matrices with low singular values because they will add little information. This way we may obtain a very good approximation of \(\mathbf{A}\) using only a fraction of the columns and rows of \(\mathbf{U}\), \(\mathbf{\Sigma}\) and \(\mathbf{V}^T\). This technique is used for instance in lossy image compression.
\(\mathbf{U}\) is an Eigenbasis of \(\mathbf{AA}^T\)
One more thing, before we are done. You should know that \(\mathbf{U}\) is the basis of \(\mathbf{AA}^T\). To see this we find the relationship between \(\mathbf{U}\) and \(\mathbf{A}\mathbf{A}^\top\), for that we simply multiply \(\mathbf{A}\) by its transpose and substitute it into the formula for the SVD:
\[\mathbf{A}\mathbf{A}^\top = (\mathbf{U}\mathbf{\Sigma}\mathbf{V}^\top)(\mathbf{U}\mathbf{\Sigma}\mathbf{V}^\top)^\top\]
Then we apply the transpose rule \((\mathbf{ABC})^\mathbf{T} = \mathbf{C}^\mathbf{T} \mathbf{B}^\mathbf{T} \mathbf{A}^\mathbf{T}\):
\[\mathbf{A}\mathbf{A}^\top = (\mathbf{U}\mathbf{\Sigma}\mathbf{V}^\top)(\mathbf{V}\mathbf{\Sigma}^\top\mathbf{U}^\top)\]
and simplify using orthogonality. Since \(\mathbf{V}\) is an orthogonal matrix, \(\mathbf{V}^\top\mathbf{V} = \mathbf{I}\):
\[\mathbf{A}\mathbf{A}^\top = \mathbf{U}\mathbf{\Sigma}(\mathbf{V}^\top\mathbf{V})\mathbf{\Sigma}^\top\mathbf{U}^\top = \mathbf{U}\mathbf{\Sigma}\mathbf{\Sigma}^\top\mathbf{U}^\top\]
Let \(\mathbf{\Lambda} = \mathbf{\Sigma}\mathbf{\Sigma}^\top\). Since \(\mathbf{\Sigma}\) is diagonal, \(\mathbf{\Lambda}\) is also a diagonal matrix containing the squares of the singular values (\(\sigma_i^2\)).
\[\mathbf{A}\mathbf{A}^\top = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^\top\]
This is the spectral decomposition of \(\mathbf{A}\mathbf{A}^\top\), confirming that \(\mathbf{U}\) is indeed its eigenbasis. It is worth pausing here to note a satisfying and non-obvious fact: the nonzero eigenvalues of \(\mathbf{A}\mathbf{A}^\top\) and \(\mathbf{A}^T\mathbf{A}\) are identical. Both equal \(\sigma_i^2\), the squares of the singular values. This means that even though \(\mathbf{A}\mathbf{A}^\top \in \mathbb{R}^{m \times m}\) and \(\mathbf{A}^T\mathbf{A} \in \mathbb{R}^{n \times n}\) may have different sizes, they share the same nonzero eigenvalues. The two symmetric matrices are in this sense two sides of the same coin, with \(\mathbf{U}\) and \(\mathbf{V}\) as their respective eigenbases and the singular values \(\sigma_i\) as the bridge between them.
SVD — Summary
You made it! Let’s just do a quick recap.
The SVD is a Factorization: The SVD is a factorization method. That means it allows us to express a matrix A as a product of other matrices. In case of the SVD it’s a product of three special matrices, \(\mathbf{U}\), \(\mathbf{\Sigma}\), and \(\mathbf{V}^T\), thus we have: \[\mathbf{A} = \mathbf{U \Sigma V}^T\]
The SVD is an X-Ray These \(\mathbf{U}\), \(\mathbf{\Sigma}\), \(\mathbf{V}^T\) represent geometrical transformations, a rotation, a stretch and another rotation. Thus, the SVD proves that any linear transformation (any matrix), no matter how complex, can be simplified into this clean three-step sequence of rotation, stretch and rotation. This is an absolutely remarkable insight! Every matrix, regardless of its shape, is just a combination of these three simple operations. Take a moment to let that sink in.
Thus, when we see a matrix – depending on our level of expertise – we might see a grid of numbers, or – if we are more advanced – we might see a collection of vectors or linear equations. But the SVD breaks it down into this elegant three-step sequence. It is like an X-Ray that reveals this structure from a cluttered grid of numbers.
The SVD Allows Decomposition by Relevance We can represent the product \(\mathbf{A} = \mathbf{U \Sigma V}^T\) as a sum of simpler matrices, each weighted by its significance. This is the core aspect of the SVD regarding applications: again – it allows us to decompose a matrix into its components ordered by their relevance. This feature serves as the foundation of PCA.
By summing only the most important matrices and discarding those with low weights (the “noise”), we can efficiently approximate our original matrix. This capability is what enables modern data compression.
The SVD is a Swiss Army Knife: The truly special aspect about SVD is not even that it decomposes a matrix into its elementary parts and identifies their significance, but that it does so for any matrix.
References
[1] Gilbert Strang. Introduction to Linear Algebra, Fifth Edition. Wellesley-Cambridge Press, 2016.
[2] see here for a great video on spectral decomposition
[3] see here for a great video on svd
Discover more from Master the Math
Subscribe to get the latest posts sent to your email.