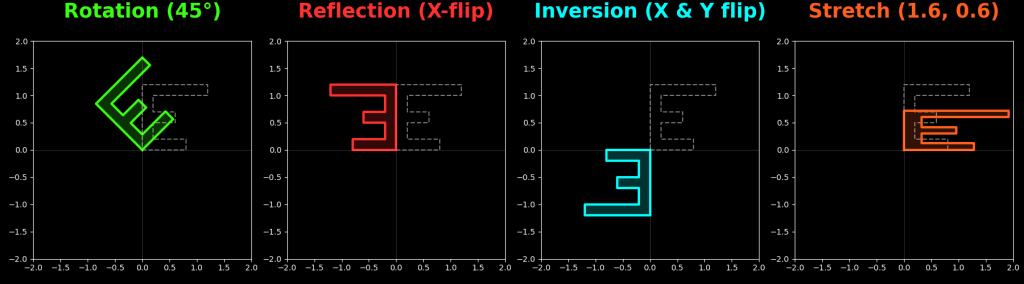
In applications like the Singular Value Decomposition (SVD), a linear transformation is typically described as a sequence of three geometric steps: a rotation, a stretch, and a final rotation. Textbooks tell us that for the rotation we need an orthogonal matrix and for the stretch we need a diagonal matrix. (Just to be precise: an orthogonal matrix cannot only rotate, it can also reflect, i.e. mirror, and a diagonal matrix cannot only stretch, it can also invert, cf. Figure 1.) The goal of this article is to understand why orthogonal matrices and diagonal matrices are restricted to perform only these specific linear transformations.

Why do orthogonal matrices perform rotations or reflections?

Orthogonal matrices maintain inner products. This is the key information. Here is the proof: An orthogonal matrix \(\mathbf{Q}\) is defined by \(\mathbf{Q}^\text{T} \mathbf{Q} = \mathbf{I}\). This property ensures that if we transform two vectors \(\mathbf{x}\) and \(\mathbf{y}\), their inner product remains invariant: \[(\mathbf{Q}\mathbf{x}) \cdot (\mathbf{Q}\mathbf{y}) = (\mathbf{Q}\mathbf{x})^\text{T} (\mathbf{Q}\mathbf{y}) = \mathbf{x}^\text{T} \mathbf{Q}^\text{T} \mathbf{Q} \mathbf{y} = \mathbf{x}^\text{T} \mathbf{I} \mathbf{y} = \mathbf{x} \cdot \mathbf{y}\] But why does this mean that we can only do rotations or reflections? Because when the inner products are preserved then it follows that:

1. Lengths are preserved: Since \(\|\mathbf{Q}\mathbf{x}\| = \|\mathbf{x}\|\), the transformation is an isometry—it cannot scale or distort the size of objects.

2. Angles are preserved: Because the dot product and lengths are constant, the angle \(\theta\) between vectors remains unchanged.

Thus, if your operation cannot change lengths or angles, then all it can do is to rotate or reflect.

Why do diagonal matrices perform stretching and inversion?

If you multiply a matrix with a vector this can be written as a sum of the columns of the matrix weighted by the entries of the vector. But since each column of a diagonal matrix is 0 everywhere except for one position that lies on the diagonal we will observe the following: \[\begin{bmatrix} x_1 & 0 & \cdots & \\ 0 & x_2 & & \\ & \cdots & & \\ \cdots & & &x_n \end{bmatrix} \begin{bmatrix} \alpha_1\\ \vdots \end{bmatrix} = \alpha_1 \begin{bmatrix} x_1 \\ 0 \\ \vdots \\ \end{bmatrix} + \alpha_2 \begin{bmatrix} 0 \\ x_2 \\ \vdots \\ \end{bmatrix} \cdots = \begin{bmatrix} \alpha_1 x_1\\ \vdots\\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ \alpha_2 x_2\\ \vdots\\ \end{bmatrix} + \cdots = \begin{bmatrix} \alpha_1 x_1\\ \alpha_2 x_2\\ \vdots\\ \alpha_n x_n\\ \end{bmatrix} \label{eq:stretch}\] As you can see from the above equation the result of multiplying a diagonal matrix by a vector is a vector where each component is multiplied (i.e. stretched, or reflected if the sign of the entry in the diagonal matrix is negative) by the corresponding diagonal entry of the matrix. Thus, when a diagonal matrix multiplies a vector this reduces to multiplying the \(i\)’th component of the vector with the \((i,i)\)’th entry in the matrix. You will obtain an inversion if one of the diagonal values is negative. In SVD these diagonal elements are the singular values and by convention they are chosen to be positive, thus there you will have a pure stretch.

Summary

We have seen that orthogonal matrices are restricted to rotations or reflections because they preserve inner products. Diagonal matrices stretch (or invert) space because they are the only way to scale the components of a vector independently.