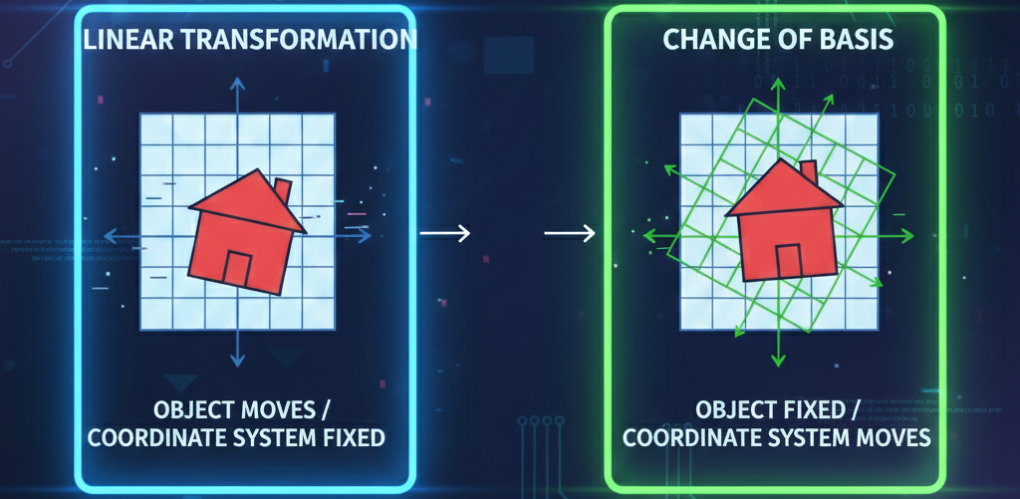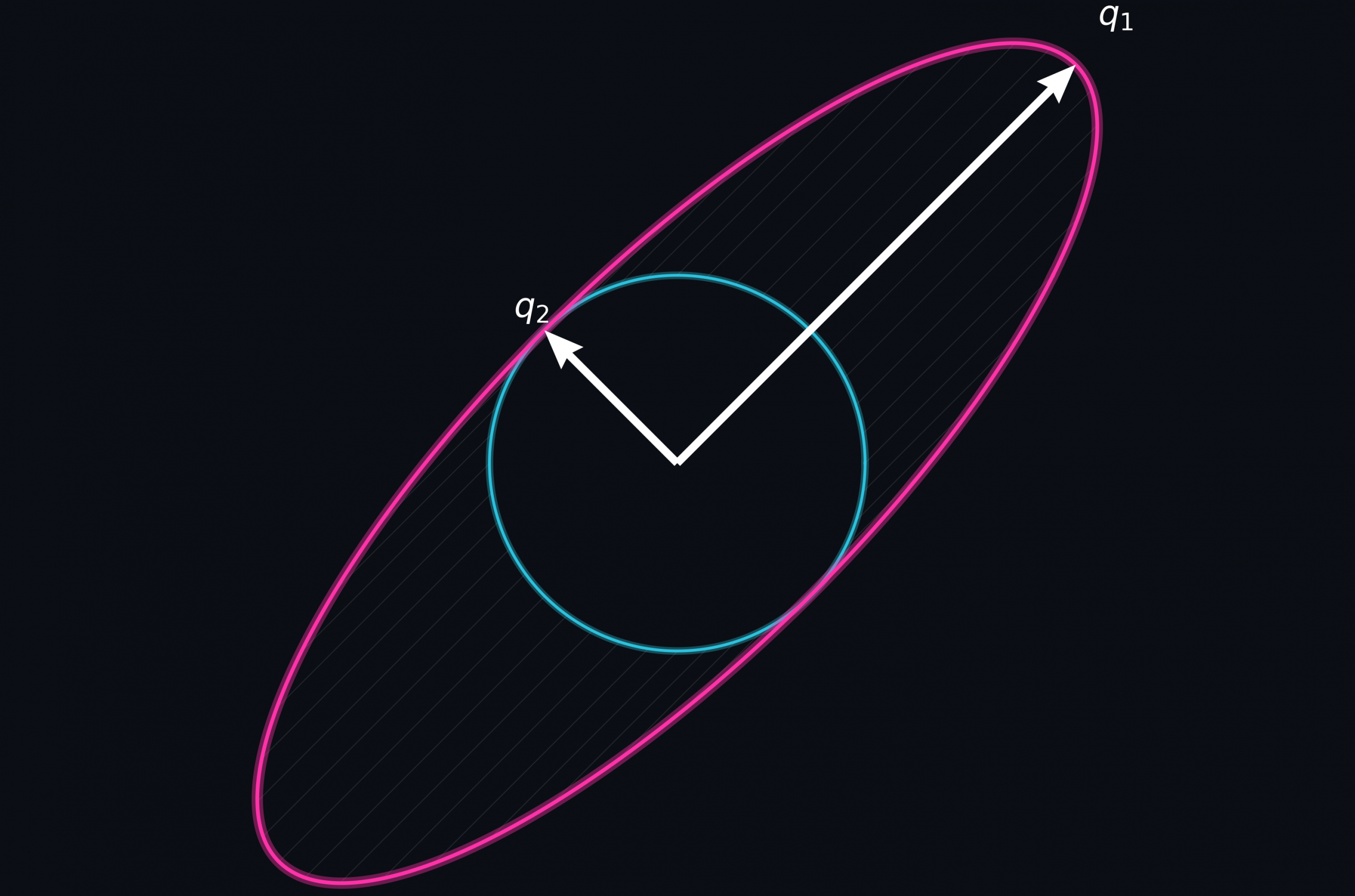
Introduction

Diagonalization is the process that enables us to decompose certain square matrices into the product of three matrices as we’ve covered here. However, not all matrices are diagonalizable, and usually, several checks are required to determine eligibility. But, when a real matrix is symmetric, it can always be diagonalized. This specific process is called spectral decomposition which this article is about. Another great resource is this video.

The spectral theorem (or principal axes theorem) ( p. 339) provides the theoretical justification for this, stating that a symmetric matrix is:

1. Unconditionally diagonalizable.

2. Diagonalizable using an orthonormal basis of eigenvectors.

Let’s look at the difference between standard diagonalization and spectral decomposition: Standard diagonalization factors a matrix \(\mathbf{A}\) into:\[\mathbf{A} = \mathbf{X \Lambda X}^{-1}\] where \(\mathbf{X}\) is the eigenbasis and \(\mathbf{\Lambda}\) is the diagonal matrix of eigenvalues. In this case, the eigenvectors in \(\mathbf{X}\) do not have to be orthogonal. In spectral decomposition, this simplifies to: \[\mathbf{S} = \mathbf{Q \Lambda Q}^T\] where \(\mathbf{Q}\) denotes the orthonormal eigenvectors of \(\mathbf{S}\). Because \(\mathbf{S}\) is symmetric, we are guaranteed that these eigenvectors are orthonormal. This allows us to use the transpose \(\mathbf{Q}^T\) instead of the inverse \(\mathbf{Q}^{-1}\) and we’ll see why in section 3. Let’s look at symmetric matrices first.

The Symmetric Matrix

A symmetric matrix \(\mathbf{S}\) is defined as a square matrix that equals its own transpose: \[\mathbf{S} = \mathbf{S}^T\] This symmetry implies that the entries are mirrored across the main diagonal of the matrix as shown in Figure 1.

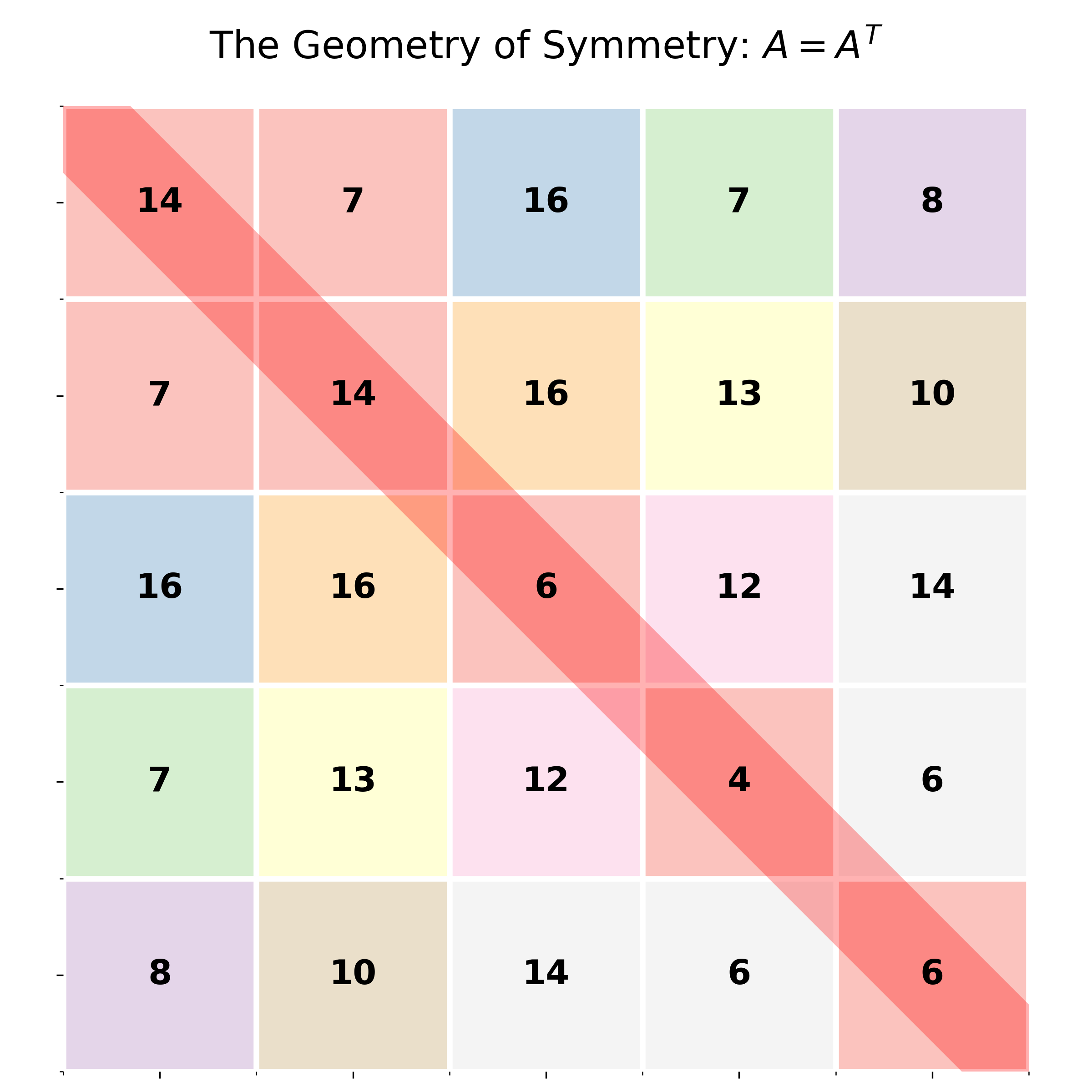
Two properties are particularly relevant:

• Every diagonal matrix is symmetric.

• The product \(\mathbf{A}^T \mathbf{A}\) is symmetric for any matrix \(\mathbf{A} \in \mathbb{R}^{m \times n}\).

We verify the second property as follows:\[(\mathbf{A}^T \mathbf{A})^T = \mathbf{A}^T (\mathbf{A}^T)^T = \mathbf{A}^T \mathbf{A}\]

Using the Spectral Theorem to go from Diagonalization to Spectral Decomposition

The spectral theorem ensures that for a symmetric matrix, the eigenvectors are orthogonal. Since we can normalize these vectors to length 1, they become orthonormal.

For any orthonormal matrix \(\mathbf{Q}\), the following property holds: \[\mathbf{Q}^T \mathbf{Q} = \mathbf{I}\] This is because the dot product of a vector of an orthonormal matrix with itself is 1 (\(\mathbf{q}_i^T \mathbf{q}_i = 1\)), while the dot product between different vectors is 0 (\(\mathbf{q}_i^T \mathbf{q}_j = 0\)). If in addition the matrix is also square it implies that \[\mathbf{QQ}^T = \mathbf{I}\] Since \(\mathbf{Q}^T \mathbf{Q} = \mathbf{I} =\mathbf{QQ}^T\), it follows that \(\mathbf{Q}^T = \mathbf{Q}^{-1}\). (Because by definition, a matrix \(\mathbf{B}\) is the inverse of \(\mathbf{A}\) if it satisfies the two-sided relation \(\mathbf{AB} = \mathbf{BA} = \mathbf{I}\).) Substituting this into the diagonalization formula \(\mathbf{S} = \mathbf{Q \Lambda Q}^{-1}\), we arrive at: \[\mathbf{S} = \mathbf{Q \Lambda Q}^T\] Why is this great? It simplifies computation significantly: we avoid the expensive calculation of a matrix inverse and instead use the transpose, which is faster and numerically more stable.

Now that we know how the spectral decomposition is derived algebraically, let’s gain a deeper understanding of it by looking at what actually happens geometrically during spectral decomposition.

The Geometry of the Spectral Decomposition

Diagonalization is a sequence of geometric transformations, namely a change of basis, a stretch and another change of basis. Because \(Q\) is orthogonal, the change of basis reduces to a rigid transformation, i.e. a transformation that preserves lengths and angles, that means it can’t stretch or distort the space, only rotate or reflect it. Why?.

If we apply S to some vector x we can write: \[\begin{equation} \mathbf{Sx} = \mathbf{Q}(\mathbf{\Lambda}(\mathbf{Q}^T\mathbf{x})) \end{equation}\] Let’s go through the steps, which are also illustrated in Figure 2.

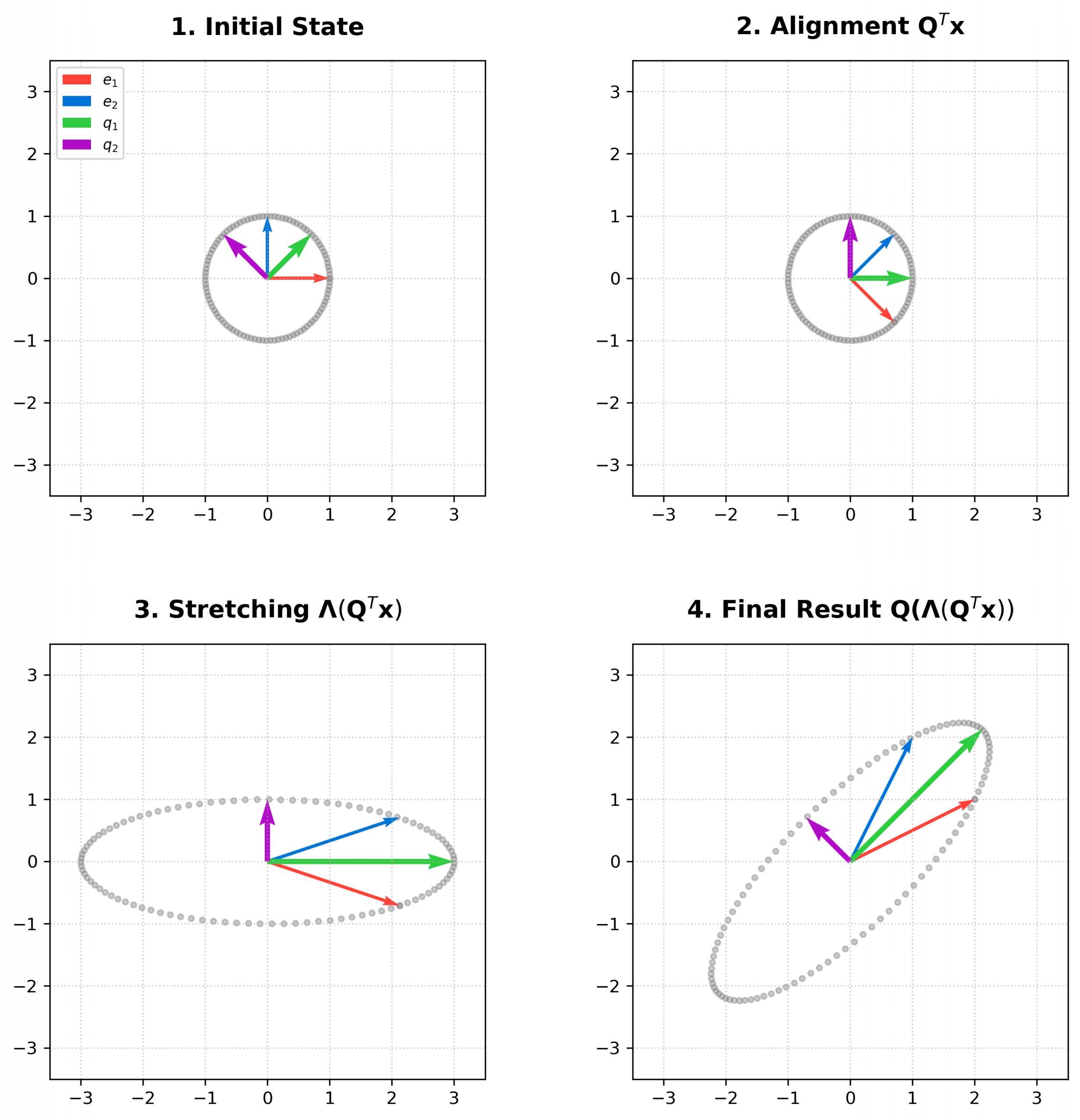
1. The first transformation (\(\mathbf{Q}^\text{T} \mathbf{x}\)): \(\mathbf{Q}^\text{T}\) acts as a rotation or reflection. What does it do to the eigenvectors? Any idea? It aligns the eigenvectors with the standard basis. To see why this happens, consider \(\mathbf{Q}\) in 2 dimensions with eigenvectors \(\mathbf{q}_1\) and \(\mathbf{q}_2\):\[\mathbf{Q} = \begin{bmatrix} | & | \\ \mathbf{q}_1 & \mathbf{q}_2 \\ | & | \end{bmatrix}\] The transpose \(\mathbf{Q}^\text{T}\) places these eigenvectors in the rows: \[\mathbf{Q}^\text{T} = \begin{bmatrix} — \mathbf{q}_1^\text{T} — \\ — \mathbf{q}_2^\text{T} — \end{bmatrix}\] When we multiply an eigenvector by \(\mathbf{Q}^\text{T}\), we calculate:

   \[\mathbf{Q}^\text{T} \mathbf{q}_1 = \begin{bmatrix} \mathbf{q}_1^\text{T} \mathbf{q}_1 \\ \mathbf{q}_2^\text{T} \mathbf{q}_1 \end{bmatrix}\] Because the eigenvectors are orthonormal, the following properties apply:

   The dot product of a vector with itself is 1 (\(\mathbf{q}_1^\text{T} \mathbf{q}_1 = 1\)).

   The dot product between different eigenvectors is 0 (\(\mathbf{q}_2^\text{T} \mathbf{q}_1 = 0\)). Therefore, \(\mathbf{Q}^\text{T} \mathbf{q}_1 = [1, 0]^\text{T} = \mathbf{e}_1\). As shown in the top right of Figure 2, \(\mathbf{Q}^\text{T}\) “snaps” the matrix’s natural basis back to the standard basis. The circular shape remains intact because this rigid motion does not stretch the space.

2. The stretching (\(\mathbf{\Lambda}(\mathbf{Q}^\text{T} \mathbf{x})\)): Once aligned with the axes, \(\mathbf{\Lambda}\) stretches the space along these axes according to the eigenvalues \(\lambda_i\). This is shown in the lower left of Figure 2. Every vector is stretched in the direction of the principal axes (the eigenvectors). The resulting shape is an ellipse (or hyper-ellipsoid) where the major and minor axes are currently aligned with the standard basis vectors.

3. Rotating back (\(\mathbf{Q}(\mathbf{\Lambda}(\mathbf{Q}^\text{T} \mathbf{x}))\)): The final multiplication by \(\mathbf{Q}\) rotates the stretched shape back to the original coordinate system. The lower right of Figure 2 illustrates this result. Look at the eigenvectors. Compare their directions with the directions in the top left picture. They haven’t changed! Their lengths have of course, but not their directions. This is the definition of eigenvectors: when multiplied by \(\mathbf{S}\), the vector stays on its own span, only its length changes.

From Theory to Praxis

Here is some python code to demonstrate how to use spectral decomposition:

import numpy as np

# 1. Create a symmetric matrix S
S = np.array([[6, 2],
              [2, 3]])
print("Symmetric Matrix S:\n", S)

# 2. Compute eigenvalues (L_vals) and eigenvectors (Q)
# np.linalg.eigh is optimized for Symmetric/Hermitian matrices
L_vals, Q = np.linalg.eigh(S)

# 3. Create the diagonal matrix Lambda
Lambda = np.diag(L_vals)

# 4. Reconstruct the matrix: S = Q @ Lambda @ Q.T
S_reconstructed = Q @ Lambda @ Q.T

print("\nEigenvalues (L_vals):\n", L_vals)
print("\nOrthonormal Eigenvectors (Q):\n", Q)
print("\nReconstructed S:\n", S_reconstructed)

# 5. Quick Verification: Q.T @ Q should be the Identity matrix
print("\nVerification (Q.T @ Q ~= I):\n", np.round(Q.T @ Q, 10))

Conclusion

This is it! You now understand that spectral decomposition is the diagonalization of real symmetric matrices, where the eigenvectors are guaranteed to be orthogonal to each other. This reduces the change of basis to a rigid motion—a rotation or a reflection.

The spectral decomposition allows us — like an x-ray — to clearly see the internal actions of a matrix. When applied to a shape, such as a unit sphere, the process can be summarized as follows:

• Alignment: It first expresses all vectors of the shape in the matrix’s natural basis (its eigenvectors). Geometrically, this is equivalent to aligning the eigenvectors with the standard basis.

• Scaling: The shape is then stretched or compressed along these axes according to the respective eigenvalues.

• Restoration: Finally, the shape is rotated or reflected back to the original coordinate system.

By breaking a complex transformation into these intuitive geometric steps, spectral decomposition provides a powerful lens for understanding how symmetric matrices operate in higher-dimensional spaces.

Appendix

Orthogonal matrices preserve inner products. An orthogonal matrix \(\mathbf{Q}\) is defined by the property \(\mathbf{Q}^\text{T} \mathbf{Q} = \mathbf{I}\). This means that if we transform two vectors \(\mathbf{x}\) and \(\mathbf{y}\), their inner product remains unchanged: \[(\mathbf{Q}\mathbf{x}) \cdot (\mathbf{Q}\mathbf{y}) = (\mathbf{Q}\mathbf{x})^\text{T} (\mathbf{Q}\mathbf{y}) = \mathbf{x}^\text{T} \mathbf{Q}^\text{T} \mathbf{Q} \mathbf{y} = \mathbf{x}^\text{T} \mathbf{I} \mathbf{y} = \mathbf{x} \cdot \mathbf{y}\] Two important implications follow from the fact that the inner product is preserved:

1. Lengths are preserved: If we consider the case where \(\mathbf{x} = \mathbf{y}\), then \(\|\mathbf{Q}\mathbf{x}\| = \|\mathbf{x}\|\). The transformation does not scale the vector.

2. Angles are preserved: Since the dot product is defined as \(\mathbf{x} \cdot \mathbf{y} = \|\mathbf{x}\| \|\mathbf{y}\| \cos(\theta)\), and both the lengths and the dot product remain constant, the angle \(\theta\) between any two vectors must also remain constant.

Because lengths and angles are preserved, the transformation induced by an orthogonal matrix cannot stretch, squash, or bend the space. It can only move the space rigidly. In linear algebra, such a transformation is called an isometry, which manifests as either a Rotation: If \(\det(\mathbf{Q}) = 1\), the orientation (handedness) of the space is preserved. Or as a Reflection: If \(\det(\mathbf{Q}) = -1\), the space is flipped or mirrored. In the context of spectral decomposition, both operations ensure that the eigenvectors remain perpendicular and of unit length during the change of basis.

References

[1] Gilbert Strang. Introduction to Linear Algebra, Fifth Edition. Wellesley-Cambridge
Press, 2016.