How to create a random variable with a Beta distribution from scratch, using only Uniform random variables

You can use software, like scipy.stats.beta if you want to sample from a Beta distribution. But you can also create a Beta distribution yourself — from scratch. The only thing you need is access to a Uniform random variable. This post shows an implementation of example 12.1.4 on p. 539 of the book “Introduction to Probability” by Blitzstein and Hwang, 2nd edition.

The task is to create a random variable with a Beta distribution with positive integers a,b by using Universality of the Uniform also known as Probability integral transform.

The Beta distribution is a continuos function over the support [0,1] and is a generalization of the Uniform distribution. A random variable, r.v. $X$ is said to have the $Beta(a,b)$ distribution if its probability density function (pdf) is:

\[\begin{equation} f(x) =x^{(a-1)}(1-x)^{(b-1)}\frac{1}{b(a,b)}\end{equation} \tag{1}\label{eq:eq1} \]
where $b(a,b)$ is a constant to make the integral of the pdf equal 1. For $(a,b)$ positive integers $b(a,b) = \frac{(a-1)!(b-1)!}{(a+b-1)!}$ (see p. 387 and 397 in [1]).

A Beta distribution can be described by two independent r.v.s $X,Y$ with the same rate $\lambda$, that have a Gamma distribution (cf. p. 396, story 8.5.1 “Bank-post office” in [1]), thus: $X / (X+Y) \sim Beta$, with $X \sim Gamma(a,\lambda)$, $Y\sim Gamma(b,\lambda)$. Here we assume $\lambda=1$. We also know that the sum of $n$ independent Gammas with the same rate $\lambda$ has a $Gamma(n,\lambda)$ distribution (p. 390, Theorem 8.4.3 in [1]), thus $X+Y$ is $Gamma(a+b,\lambda)$. Page 539 in [1] gives the solution to the task of how to simulate an r.v. with a Beta distribution:

Applying universality of the Uniform directly for the Beta is hard, so let’s first use the bank-post office story: if X~Gamma(a,1) and Y~Gamma(b,1) are independent, then X/(X+Y)~Beta(a,b). So if we can simulate the Gamma distribution, then we can simulate the Beta distribution!

To simulate X~Gamma(a,1), wen can use X1+X2+..Xa with the $X_j$ i.i.d. Expo(1) r.v.s. […] Lastly, by taking the inverse of the Expo(1) CDF and applying universality of the Uniform, -log(1-U)~Expo(1) for U~Unif(0,1), so we can easily construct as many Expo(1) r.v.s as we want.

In other words, if we want a Beta r.v. we need 2 independent Gammas with the same rate $\lambda$ (here we simply choose $\lambda=1$). And to get the Gammas we use the fact that the sum of exponentially distributed r.v.s with the same rate $\lambda$ is a Gamma r.v. We can create r.v.s that have an exponential distribution ($Expo(\lambda)$, here $\lambda = 1$), by using Universality of the Uniform. The pdf for a r.v. with an exponential distribution is $f(x)$ = $\lambda e^{(-\lambda x)}$. Universality of the Uniform says that we can create a r.v. with any desired distribution if we know the inverse of its Cumulative Distribution Function (CDF),$ F^{-1}$ and plug in a Uniform r.v. The CDF of $Expo(\lambda)$ = $F(x) = 1-e^{(-\lambda x)}$ and thus the inverse is $F^{-1} = -log(1-U)$. U is a r.v. with the Uniform distribution.

So here is the plan of attack:

1. we need acces to a r.v. with a Uniform distribution. From that we draw many samples.
2. then we plug in each of these samples into F^(-1) to get our Expo(1)
3. We repeat this $a$ times, to create $a$ exponential variables.
4. We repeat this $b$ times to create $b$ more exponential variables.
5. We sum the $a$ exponentials to get a r.v. $X\sim Gamma(a,1)$
6. We sum the $b$ exponentials to get a r.v. $Y\sim Gamma(b,1)$
7. We compute $X / (X+Y) \sim Beta(a,b)$

Now, let’s translate our plan into code. Here, I used Python. All of the steps of the plan of attack are labeled in the code.

    def do_Beta_Universality_Uniform(self)->np.ndarray:
        """
        Creates an array with samples from the desired beta(a,b) distribution.

        Returns
        -------
        beta_rv : numpy.ndarray
            an array with samples from the desired beta(a,b) distribution.

        """
        # 1) Create "a" and "b" many Expos by drawing n samples
        # from the Uniform distr. and plugging them into F^(1) of the
        #Expo (-log(1-U))
        n = self.number_of_simulations
        X = []
        for i in np.arange(self.a): #number 3 of plan of attack
            uniform_samples = uniform().rvs(size=n) #number 1 and 2 of plan of attack
            X.append((-1*np.log(1-uniform_samples)))
        Y = []
        for i in np.arange(self.b): #number 4 of plan of attack
            uniform_samples = uniform(0, 1).rvs(size=n) #number 1 and 2 of plan of attack
            Y.append(-1*np.log(1-uniform_samples))

        #5 of plan of attack - create Gamma(a,1) from Expos by summing all      
        #the a uniforms samples
        X = np.array(X)
        X = X.sum(axis=0)
        
        #6 of plan of attack - create Gamma(b,1) from Expos by summing all  
        #the b uniform samples
        Y = np.array(Y)
        Y = Y.sum(axis=0)

        #7 of plan of attack -the final Beta r.v. is X/(X+Y)
        beta_rv = X/(X+Y)

        return beta_rv

See here for a notebook with a full implementation.

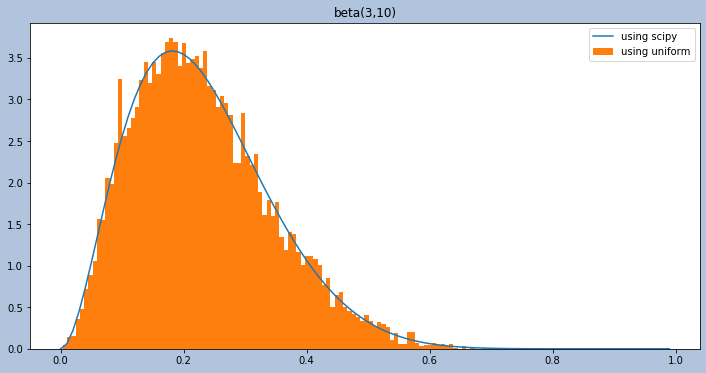
Here the variable beta_rv is a collection of samples drawn from a r.v. with a beta(a,b) distribution. To see the shape of the pdf we plot its histogram below (assuming $a=3$ and $b=10$). The equivalent scipy.stats.beta pdf is plotted in blue for comparison.

References:

[1]

William James (1890) The Principles of Psychology, New York 1(2), Robert Maynard Hutchins (ed.), p. 696, Holt, url, doi:10.1037/10538-000

Joseph K. Blitzstein, Jessica Hwang (2019) Introduction to Probability, Second Edition, Introduction to Probability, Second Edition, doi:10.1201/9780429428357

Was this helpful?

YesNo

2 / 0