A detailed solution for a problem about total probability
This article tackles problem number 7 of chapter 9 from the book “Introduction to Probability” by Blitzstein and Hwang, second edition. A solution for this problem has been published by the authors, but it’s often hard to translate a worded problem into formulas. Therefore, here, I put a lot of emphasis onto how to achieve this using this problem as example.
The problem is restated here for convenience:
“You get to choose between two envelopes, each of which contains a check for some positive amount of money. […] assume that the two values were generated independently from some distribution on the positive real numbers, with no information given about what the distribution is.
After picking an envelope, you can open it and see how much money is inside (call this value x), and then you have the option of switching. As no information has been given about the distribution, it may seem impossible to have better than a 50% chance of picking the better envelope. Intuitively, we may want to switch if x is “small” and not switch if x is “large”, but how do we define “small” and “large” […]?
Consider the following strategy for deciding whether to switch. Generate a threshold T~Expo(1), and switch envelopes if and only if the observed value x is less than the value of T. Show that this strategy succeeds in picking the envelope with more money with probability strictly greater than 1/2.”
Let’s very carefully identify what exactly is asked for in the problem. It says: “Show that this strategy succeeds in picking the envelope with more money with probability strictly greater than 1/2”.
So this would be: P(success) > 1/2. And “success” means that we end up with the envelope with more money – no matter which amount we started off with originally. We first randomly pick an envelope and we are allowed to check the amount of money it contains. We draw a sample from the random variable T and call the value of that sample t. Then we compare t to the amount of money. So this is a two staged experiment, where each stage has two possible outcomes. The possible cases are:
- We initially pick the larger amount of money, if this amount is $\ge$ t we are successful.
- We initially pick the larger amount of money, if this amount is $<$ t we fail.
- We initially pick the lesser amount of money, if this amount is $<$ t we are successful.
- We initially pick the lesser amount of money, if this amount is $\ge$ t we fail.
Let’s try to translate this into something more formal. We call the event ‘successful’ ‘G’ and we denote the larger amount of money ‘b’ and the lesser amount ‘a’. We call the event that we initially pick b ‘B’ and the event the we initially pick a ‘A’ (as done in the solution provided by the authors). Additionally we call the event when we are not successfull as ‘L’. With this, the first case translates into: We want the event $B$ to occur and we also want $G$ to happen, so we are interested in $B \cap G$. Per definition of the joint probability of two events the probability of this is: $P(B)*P(G|B)$. The other cases are analogous and are listed below:
- $P(B \cap G)$ = $P(B) P(G|B)$
- $P(B \cap L)$ = $P(B) P(L|B)$
- $P(A \cap G)$ = $P(A) P(G|A)$
- $P(A \cap L)$ = $P(A) P(L|A)$
This two-staged experiment can be visualized by the probability tree shown in fig. 2 below. Since we are interested in the total probability of all the events in which we are successful, we simply need to add the branches that are highlighted in purple, thus:
$P(G) = P(A)*P(G|A) + P(B)*P(G|B)$ and we want to show that this is $\gt 1/2$.
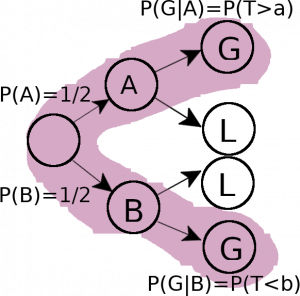
Fig.2: Probability tree that describes the two staged experiment. All branches ending in success are highlighted in purple.
Now that we know what we need to compute, we are left with the task of determining the required probabilities. We already know that $P(A) = P(B)=1/2$, because there is no reason to prefer picking one envelope to the other. But what is $P(G|A)$? For this we use the information given in the problem statement. It is said that we compare the amount of money in the envelope to the value $t$ which is the outcome of a random experiment following an Exponential distribution. So G given A will happen if the value t is larger than the value a. What is the probability that t>a? It is given by $P(T>a)$. Realize that ‘T’ is a random varible and ‘a’ is a number. Note, that we could not say P(A<t) because ‘A’ is an event and ‘t’ a number. Because we know T’s distribution ($T \sim Expo(1)$) we know that:
\begin{equation}P(G|A) = P(T>a) = 1-P(T<a) = 1-(1-e^{-a}) = e^{-a}\end{equation}
Analogous to this is:
\begin{equation}P(G|B) = P(T\le b) = 1-e^{-b}\end{equation} So:
\begin{equation} P(G) = P(A)*P(G|A) + P(B)*P(G|B) = 1/2 * e^{-a} + 1/2 * 1-e^{-b} = 1/2 ( e^{-a} +1-e^{-b} ) \end{equation}
We assume that $e^{-a} +1-e^{-b} > 0$ and thus $P(G) = 1/2 ( e^{-a} +1-e^{-b} >1/2$.
This article was published at medium.
Was this helpful?
1 / 0